Tag: 期权

财经资讯

期权系列（13）：Gamma——期权的“加速度”

2 月 2, 2026 通过 XM 0 评论 #Delta, #Gamma, #投资组合, #期权, #风险管理

我们昨天文章说了Delta中性的组合赚什么钱，其中一个因素就是Gamma。那今天我们来详细说一下Gamma。

从理论定价模型上来讲，期权价格的决定因素有五个：标的价格、行权价格、标的波动率、到期时间和无风险利率。除了行权价格之外，另外四个因素的变化所导致的期权价格的变化，就分别对应了四个希腊字母，Delta、Vega、Theta和Pho。Delta及其中性咱们说过了，Theta跟时间价值衰减咱们也说过了，Pho一般研究的价值不大，因为无风险利率在一段时间内可能是相对稳定的，对期权价格影响很小；Vega是波动率的变化所导致的期权价格的变化，波动率变化对期权价格的影响咱们其实也说过，不过Vega也是可以对冲的，我们后面再说。

我们通常说期权的风险，五个希腊字母，除了上面四个外，还有一个就是Gamma，它是标的价格变化所导致的Delta的变化，而Delta是标的价格变化所导致的期权价格的变化，所以用数学语言来讲Gamma就相当于是期权价格对标的价格的二阶导数，用人话来讲就是期权价格变化的“加速度”。

比如我买一个上证50ETF3月合约2.75的看涨期权，它的Gamma长这样：

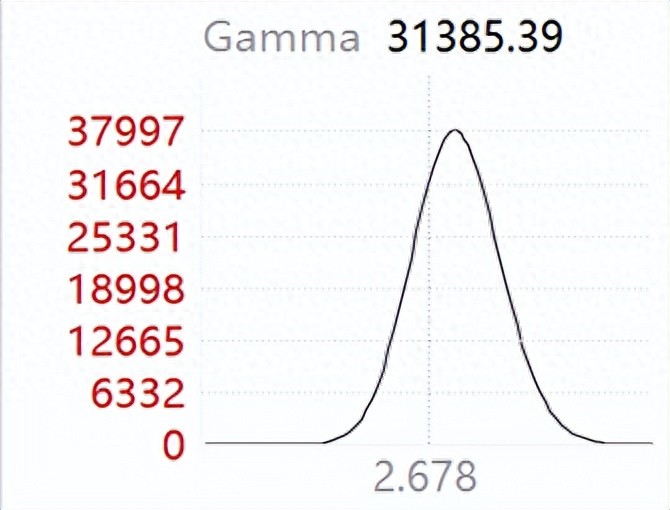
期权vega值_Gamma对期权价格的影响_期权Gamma值

上证50ETF3月合约2.75的看涨期权的Gamma

由图上可以看出Gamma随着标的价格的变动是先涨后跌的，平值期权的Gamma最大，另外就是买期权我们的Gamma是正的，那反过来卖期权Gamma就是负的了。

咱们再看一张图：

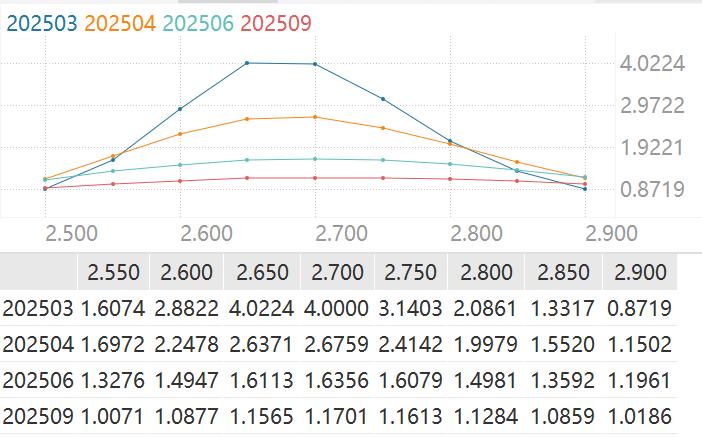
期权vega值_期权Gamma值_Gamma对期权价格的影响

不同月份不同行权价期权的Gamma

距离到期日越近的Gamma越大，越远的Gamma越小。这也容易理解，毕竟时间越远不确定性越高，对标的价格的变化会越不敏感。就像2·21那天科创50ETF2月1.3的看涨期权涨了2300%，而6月1.3看涨只涨了87.34%一样的道理。

最后咱们举个例子来看看Gamma对期权价格的影响。50ETF标的价格为2.678，如果买3月行权价为2.75的看涨期权，Delta是0.2545，Gamma是3.1403，期权价格为0.004。如果标的价格上涨0.01，在假设所有影响都线性的情况下，Gamma导致的Delta变化为0.0314，这时候Delta变成了0.2859，导致的期权价格变化为0.002859，涨幅超过70%。

所以仅依靠 Delta 来管理期权投资组合存在局限性。当标的资产价格发生较大变动时，Delta 值并非固定不变，而是会受到 Gamma 的影响而改变。这意味着，即使投资组合初始处于 Delta 中性状态，随着标的资产价格的波动，由于 Gamma 的作用，Delta 值会发生变化，组合将不再保持 Delta 中性，从而面临风险。

在实践中像做市商或者专业的期权投资机构会比较关注Gamma，普通投资者可能很难做到这么精准地管理Gamma风险。不过学习了解了这个东西总不会有坏处。明天咱们来说说专业机构会用的一种Gamma Scalping策略。

（温馨提示：文中案例仅为展示用，不作为任何投资建议。投资有风险，入市需谨慎。）

财经资讯

期权的杠杆怎么计算倍数？

2 月 1, 2026 通过 XM 0 评论 #投资, #期权, #杠杆, #计算, #风险管理

期权和期货，这两类产品都具备杠杆性，然而杠杆属性却存在差异。就期货而言，期货合约的杠杆是固定的，买卖双方都必须缴纳保证金。

但是，就期权来说，杠杆源自产品的设计本身，而且每个期权合约的杠杆率并非固定，那么到底应当如何计算期权的杠杆呢？

期权的杠杆怎么计算倍数？

一、基本公式

杠杆倍数 = 标的资产价格 /（期权价格 ×Delta）

其中，Delta 是用于衡量期权价格对标的资产价格变动敏感性的指标，其取值范围处于 – 1 到 1 之间。对于买入看涨期权，Delta 值处于 0 和 1 之间；对于买入看跌期权，Delta 值处于 – 1 和 0 之间。

二、简化公式（不考虑 Delta 值）

杠杆倍数 = 标的资产价格 / 期权价格（此公式相对粗略，未考量期权价格对标的资产价格变动的敏感性）

三、示例说明

假定某股票当下的价格是 100 元，一份行权价格为 95 元的看涨期权价格为 5 元，Delta 为 0.5。那么，该期权的杠杆倍数 = 100 /（5×0.5）= 40 倍。这表示标的资产价格每上涨 1%，期权价格理论上会上涨 40%。

再看另一示例，某看涨期权的 Delta 值为 0.6，标的资产价格为 60 元，期权价格为 3 元。那么杠杆倍数 = 0.6×（60/3）= 12 倍。

期权杠杆计算公式_期权敏感性_期权杠杆率计算方法

影响期权杠杆倍数的因素

标的资产价格：标的资产价格越高，杠杆倍数通常越低。

期权价格：期权价格越低，杠杆倍数越高。

期权类型：实值期权、平值期权和虚值期权的杠杆倍数不同。通常，虚值期权的杠杆倍数较高，但实现盈利的概率较低。

到期时间：距离到期时间越近，期权的时间价值衰减越快，杠杆倍数可能发生变化。

那么，针对于期权杠杆，如何做好管理呢？

合理控制仓位

限制投入比例：根据自身的风险承受能力和投资目标，严格控制投入期权交易的资金占总资金的比例。一般来说，建议将这一比例控制在较低水平，如不超过 20%，以防止因期权杠杆带来的巨大波动对整体资产造成严重冲击。

分散投资：不要把所有资金集中在单一的期权合约上，而是选择不同标的资产、不同到期时间、不同行权价格的期权合约进行分散投资。这样可以降低因某一特定合约出现不利变动而导致的损失风险。

科学设置止损和止盈

确定止损点：在进行期权交易前，根据自己能够承受的最大损失额度，为每一笔交易设定明确的止损点。当期权价格达到止损点时，果断平仓止损，避免损失进一步扩大。止损点的设定可以参考期权的成本、市场波动情况以及个人的风险偏好等因素。

设定止盈目标：同样，也要为交易设定合理的止盈目标。当期权价格达到预期的盈利水平时，及时获利了结，避免因贪心而错失盈利机会，甚至导致盈利回吐。止盈目标的确定可以结合市场趋势、期权的内在价值和时间价值等因素进行综合考虑。

密切关注市场动态

跟踪标的资产走势：期权价格与标的资产价格密切相关，因此要持续关注标的资产的价格变动、基本面情况以及相关行业的发展趋势。及时掌握影响标的资产价格的各种因素，如宏观经济数据、政策变化、公司财报等，以便根据市场变化及时调整投资策略。

留意波动率变化：期权的价值还受到波动率的影响，波动率上升会增加期权的价值，反之则会降低。投资者需要密切关注市场波动率的变化情况，当波动率过高或过低时，要谨慎使用杠杆，避免因波动率的不利变动而遭受损失。

期权是什么意思？

期权本质上是一份合约。合约的卖方通过收取一定费用（权利金），赋予买方在约定条件下买卖标的资产的权利。例如，投资者支付一定费用获得一份期权合约，该合约可能允许其在未来特定时间以固定价格购买某公司股票。

主要要素

标的资产：期权合约中所涉及的资产。比如沪深 300ETF 期权，其标的资产就是沪深 300 交易型开放式指数基金。

行权价格：也称为执行价格，是期权合约规定的、买方有权在未来某一时间买入或卖出标的资产的价格。例如，一份行权价格为 50 元的股票认购期权，意味着期权买方有权在规定时间内以 50 元的价格买入该股票。

到期日：期权合约有效的最后日期，过了到期日，期权就失去价值。比如一份期权的到期日是 2024 年 12 月 31 日，那么在这之后，这份期权就不再具有任何效力。

权利金：期权买方为获得期权权利而向卖方支付的费用。无论期权买方是否行使权利，权利金都不会退还。例如，投资者花费 1000 元购买一份期权，这 1000 元就是权利金。

最后，以上个人观点仅供参考，不做为买卖依据，盈亏自负。市场有风险，投资需谨慎。

财经资讯

Delta对冲后，期权和期货组合还能赚大钱吗？

1 月 30, 2026 通过 XM 0 评论 #Delta对冲, #期权, #期货, #波动率, #风险管理

在金融交易里，Delta对冲是一种常见的风险管理手段。那做完Delta对冲后，期权和期货的组合还能有明显的收益吗？

先来说说Delta对冲

Delta是期权的一个重要希腊字母，它表示期权价格对标的价格变动的敏感度。简单来说，如果一个期权的Delta是0.5，那么当标的价格上涨1块钱时，期权价格大概会上涨0.5块钱。

Delta对冲就是通过买卖标的资产（比如股票或期货），来抵消期权价格对标的价格变动的这部分风险。比如，你持有一个Delta为0.5的期权，你就可以卖空0.5份标的资产。这样，当标的价格变动时，期权价格的变化和标的资产价格的变化就会相互抵消，理论上你的组合价值就不会因为标的价格的线性变动而改变。

期权敏感性_ 期权Gamma Vega 敏感性 _Delta对冲 期货期权组合收益

Delta对冲后期货为啥没啥收益？

期货这东西，属于线性的Delta One产品。啥叫Delta One产品呢？简单理解，就是它的价格变化和标的资产价格变化是成固定比例关系的。当你对期货进行Delta对冲的时候，其实就是通过一买一卖的操作，把价格变化带来的风险给抵消掉了。

打个比方，你手里有一份期货合约，担心它价格下跌会亏钱，于是你就同时做了一笔相反方向的交易。这样，不管期货价格是涨还是跌，这两笔交易的盈亏基本就相互抵消了。对冲之后，期货组合剩下的盈亏（P&L）主要就包括carry（持有成本收益）和basis（基差），这两部分收益就像是小打小闹的“二级残差”，一般情况下，很难形成特别显著的盈利或者亏损。所以，可以这么说，期货做完Delta对冲后，基本就别指望能有什么大收益了。

期权为什么就不一样？

期权可和期货不一样，它是一种非线性的金融衍生品，和标的资产价格的关系那叫一个复杂。就算你对期权进行了Delta对冲，它还是能通过高阶项，尤其是gamma，继续保留对标的资产的风险暴露。

Gamma是啥呢？

它反映了期权价格对于标的资产价格变化的二阶敏感性。简单说，就算你把Delta对冲掉了，gamma还是会让期权的价格随着标的资产价格的变动而变动。比如说，你买了一份看涨期权，进行了Delta对冲后，当标的股票价格大幅上涨时，由于gamma的存在，期权的价格会上涨得更多；要是股票价格大幅下跌，期权价格下跌的幅度也会因为gamma而放大。

除了gamma，Vega对于期权来说也非常重要。

Vega衡量的是期权价格对于隐含波动率的敏感性。隐含波动率就像是市场对标的资产未来价格波动程度的预期。这可是期权和线性衍生品（像期货、远期等）最显著的不同之处。

对期权进行Delta对冲后，不管是gamma还是Vega带来的风险暴露，都不依赖于价格变化的方向，而是受价格变化绝对值的影响。这种风险暴露特征是没办法通过交易标的资产来复制或者消除的。

举个例子，假设你买入了一份期权并进行了Delta对冲。如果实际隐含波动率大幅增加，这意味着标的资产价格在短时间内会有剧烈的变动，不管是上涨还是下跌。这时候，期权的价格就会因为Vega的影响而大幅上涨，你就能获得显著的收益。所以，只要实际隐含波动率大幅增加，Delta对冲后的期权组合依然有可能赚大钱。

很多市场参与者不理解这一点，他们坚持靠赌方向来赢利。其实，期权设计出来就有其独特的应用场景。期权是一种对冲风险和管理波动率的工具，而不是纯粹的投机工具。如果把期权当作纯粹的投机工具，那只能祝你好运了。

期权Delta对冲后，虽然对价格变化的方向不敏感了，但仍然可以通过高阶项（尤其是gamma和vega）获得收益。只要隐含波动率发生大幅度增加，期权就可能获得显著收益。所以，期权在Delta对冲后仍然有赚钱的机会，关键是要理解期权的这些特性，而不是盲目地靠赌方向来赢利。