手把手教你计算期权价格:二项式树定价欧式看跌期权案例解析
这是《金融商品设计与评价》的第13篇文章。上一篇文章讲解了二步二项式树及其风险中性估值逻辑,没看过前面文章内容的小伙伴建议回顾之前内容。
关注我,不错过后续精彩!
期权定价听起来复杂,但如果使用二项式树(Binomial Tree)模型,整个逻辑就会变得非常直观。今天我们通过一个具体的欧式看跌期权(European Put Option)案例,完整走一遍定价流程。
期权定价的核心步骤:计算到期收益→风险中性加权→无风险贴现→回溯到初始节点。
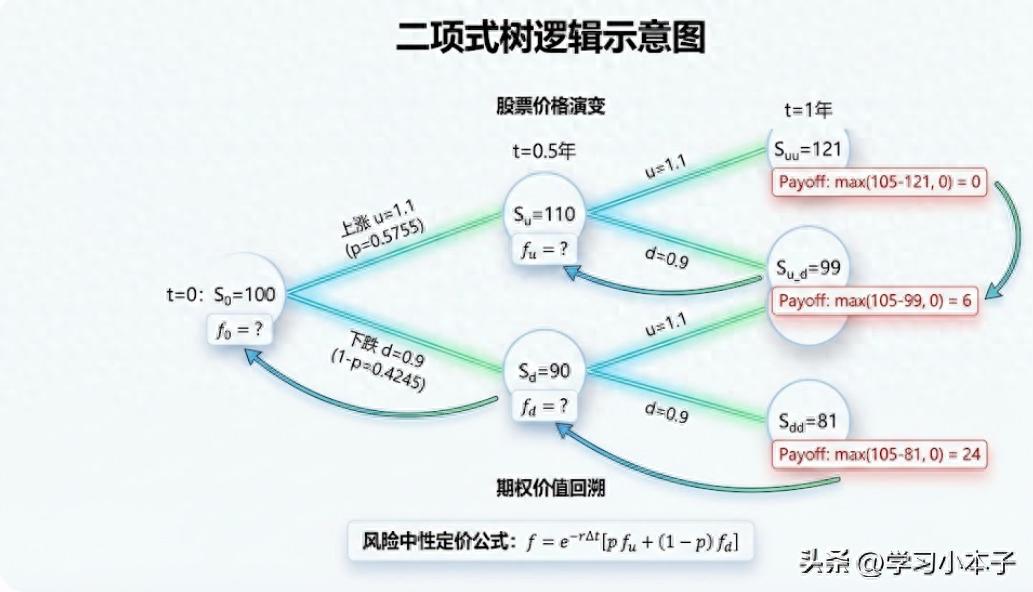
一. 案例设定
假设我们要为一个期限为1年的欧式看跌期权定价。具体的参数设定如下:
二. 计算“风险中性概率”
在二项式树模型中,最重要的中间变量是风险中性概率 (p)。它的作用是保证股票在风险中性世界中的期望增长率等于无风险利率。
代入数值:
这意味着,在风险中性世界里:
三. 股票价格与期权价值
接下来,我们需要构建二项式树,看看1年后股票价格的可能情况,以及对应的期权价值。
股票末端价格(1年后,经过两个0.5年的步长):
连续两次上涨(
):
一涨一跌(
):
连续两次下跌(
):
期权到期价值 (Payoff):
由于是看跌期权,只有当股价低于执行价(105美元)时才行权:
连续两次上涨
0 (不行权)一涨一跌
6美元连续两次下跌
24美元
二项式树逻辑示意图
四. 回溯计算现值
有了未来的价值和概率,我们可以利用期望值折现的方法,从树的末端逐步往回计算。
(注意:这里
年)
代入数值:
因此,该看跌期权的理论价值约为7.0421美元。
总结与思考
通过这个例子,我们清晰地看到了二项式树定价的全过程:
建立一个两步二项式树,对应上涨和下跌。利用风险中性概率p进行加权。先算出到期日的期权价值,再用无风险利率贴现回今天。
无论是看涨还是看跌期权,这套“回溯计算”的逻辑都是通用的。
今日互动:如果我们将波动率(上涨/下跌因子)进一步加大,而其他条件不变,你认为这个看跌期权的价格会变贵还是变便宜?
A.变贵
B.变便宜
C.不变
欢迎在评论区留下你的思考,有不懂的地方可以在评论区提出,我会一一解答。
关注我,不错过后续精彩内容!